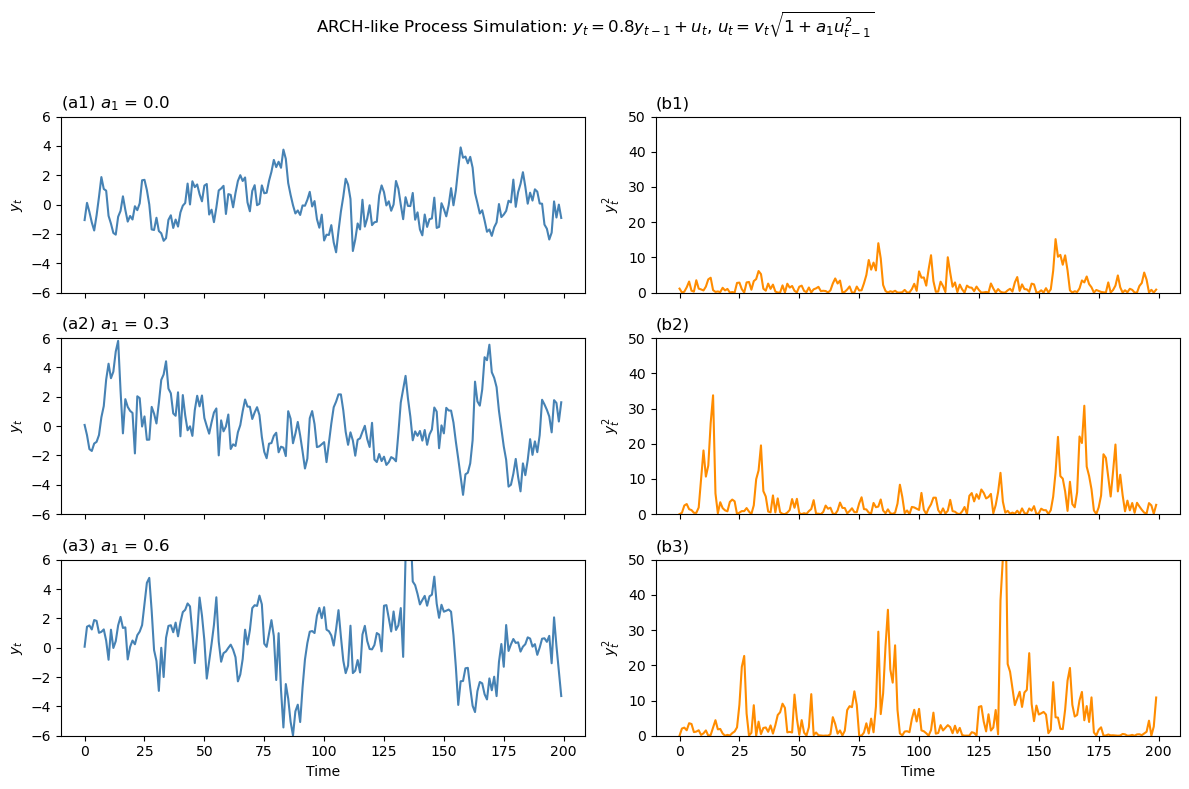
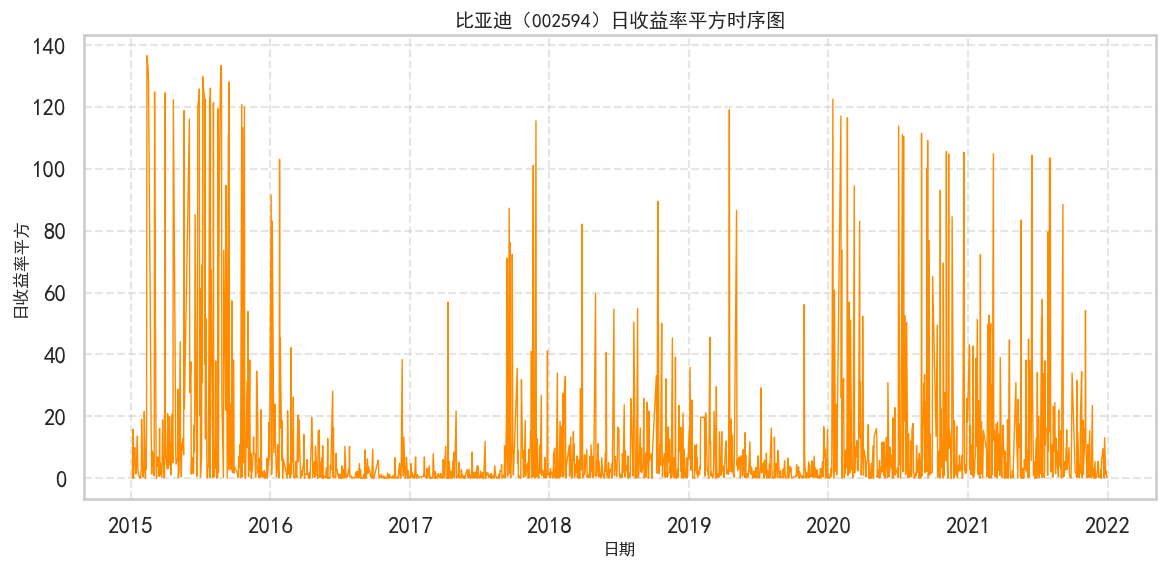
金融时间序列常常表现出不同于宏观时间序列的特征,如波动的丛聚性和分布的"尖峰厚尾"特征。传统的时间序列模型(假设干扰项的方差不随时间改变)往往无法捕捉这些特征。 Engle(1982)提出的 ARCH(auto- regressive conditional heteroskedasticity)能够较好地描述金融资产价格波动的特征,在过去的二十年里得到了广泛的应用。在实际应用中,为了达到更好的拟合效果,常常需要设定较多的滞后项来描述波动的持续性,这往往会因为参数数目过多而降低估计的有效性。
ARCH 与 GARCH
条件期望与非条件期望
Engle (1982) 提出的 ARCH 模型的基本特点是允许干扰项的条件方差随时间改变,而其非条件方差则不随时间改变。
此前我们曾提到,若一个时间序列的均值、方差或协方差是随时间改变的,那么它就是非平稳的。然而,这并不意味着条件方差随时间改变的时间序列就是非平稳的。
需要注意的是,在此前定义“非平稳过程”时,我们强调的是序列的“长期”或“非条件”均值或方差。因此,只要一个序列的非条件方差是不随时间改变的,即使其条件方差随时间改变,它仍然是平稳的。
因此,在学习 ARCH 模型过程中,我们需要区分条件期望与非条件期望,这会进一步影响序列的概率分布。在使用最大似然估计(MLE)估计计量模型时,我们往往假设序列的条件分布为正态分布。然而,序列的非条件分布往往不同于其条件分布。
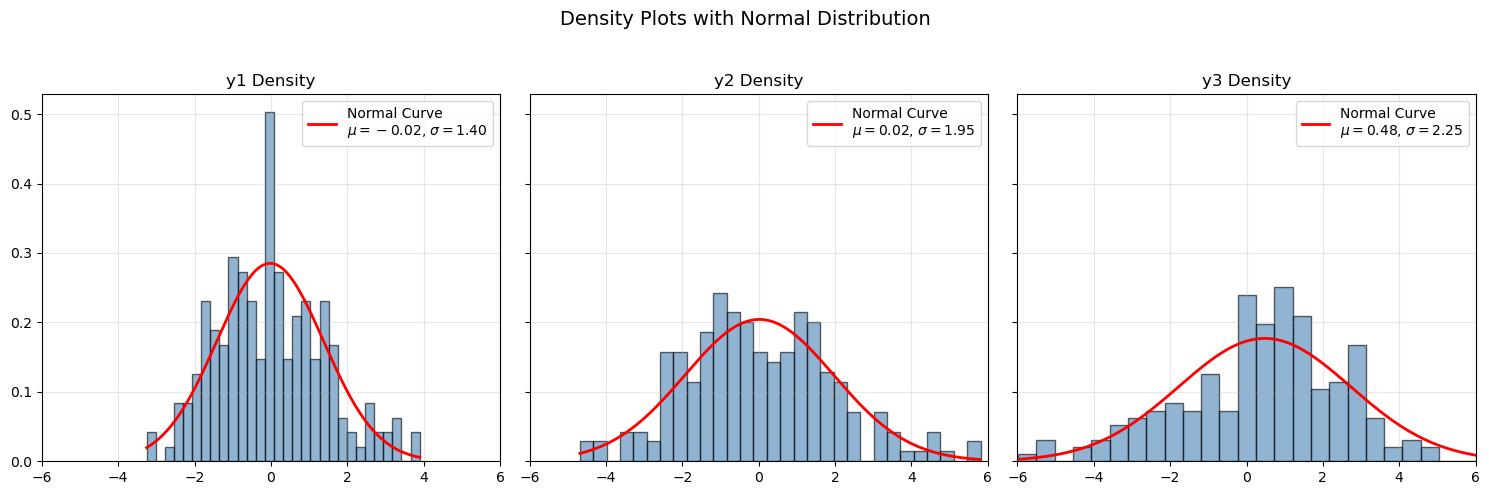
在 ARCH 模型中,若假设其条件分布为正态的,那么其非条件分布往往是非正态的,通常具有“厚尾”(fat-tails)特征。
由于大家对自回归(AR)过程已经比较熟悉,我们可以从 AR(1) 入手来解释 ARCH 模型的设定思想。考虑如下 AR(1) 模型:
\[
y_t = \rho y_{t-1} + u_t
\]
其中,\(t = 1, 2, \cdots, T\),\(u_t \sim \text{IID}(0, \sigma^2)\),并假设 \(|\rho| < 1\)。显然,\(y_t\) 是一个平稳过程,其非条件期望与方差分别为:
\[
E(y_t) = 0,\quad Var(y_t) = \frac{\sigma^2}{1 - \rho^2}
\]
若记第 \(t-1\) 期的信息集合为 \(\Omega_{t-1}\),则 \(y_t\) 的条件期望为:
\[
E(y_t \mid \Omega_{t-1}) = \rho y_{t-1}
\]
其条件方差为:
\[
Var(y_t \mid \Omega_{t-1}) = E(u_t^2 \mid \Omega_{t-1}) = \sigma^2
\]
可见,\(y_t\) 的条件期望是随时间变化的,而非条件期望则不随时间变化。
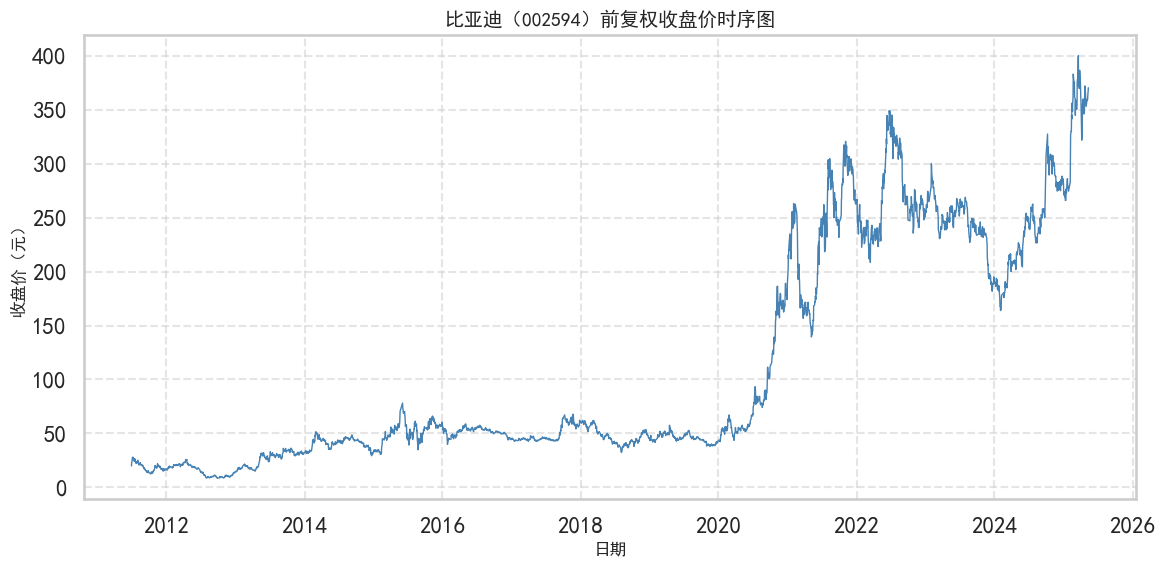
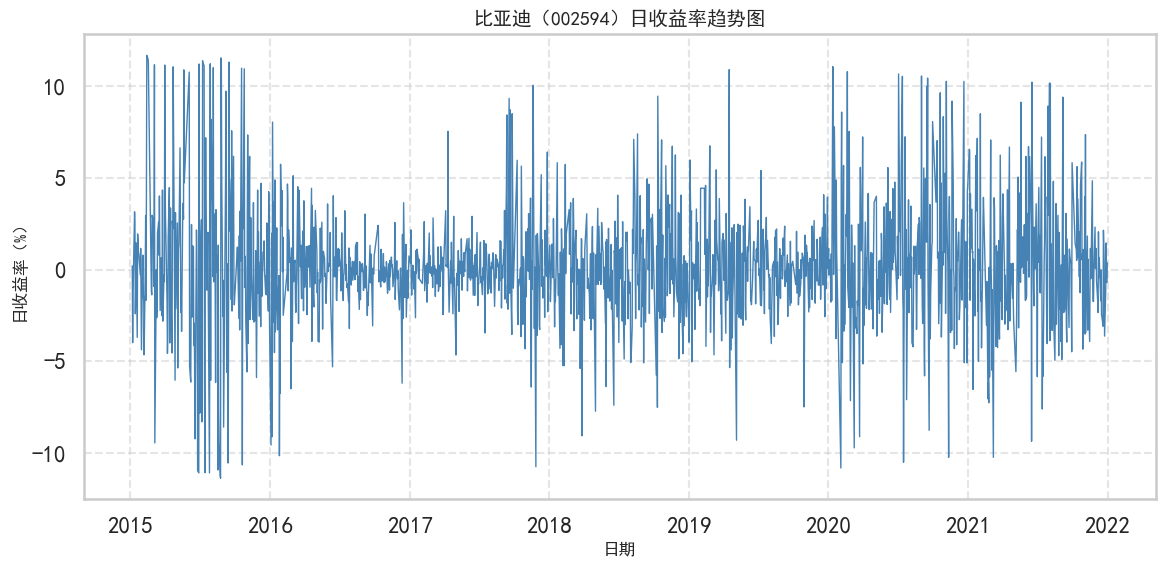
有些情况下,我们不仅需要预测时间序列的水平趋势,同时也要预测其波动情况。下图展示了上证综指的时序图,在某些时段其波动很小,而在另一些时段波动却非常剧烈。

这种波动的变化,即方差的变化,对研究金融市场的微观机制具有非常重要的意义。因为投资者在持有风险较高的资产时,往往希望获得更高的回报率作为补偿。
ARCH 模型
虽然在上面的例子中,\(u_t\) 的非条件方差是不随时间改变的,但对于多数金融时间序列而言,其条件方差往往是随时间改变的。我们可以采用如下 \(\operatorname{AR}(p)\) 过程来描述这种特征:
\[
u_t^2=\alpha_0+\alpha_1 u_{t-1}^2+\alpha_2 u_{t-2}^2+\cdots+\alpha_p u_{t-p}^2+v_t
\]
其中,\(v_t \sim \operatorname{IID} N\left(0, \sigma^2\right)\) 。由此可知,\(u_t^2\) 的条件期望为:
\[
\mathrm{E}\left(u_t^2\right)=\alpha_0+\alpha_1 u_{t-1}^2+\alpha_2 u_{t-2}^2+\cdots+\alpha_p u_{t-p}^2
\]
满足(11-2)式的白噪声序列 \(u_t\) 称为 \(p\) 阶"自回归条件异方差"(AutoRe- gression Conditional Heteroskedastic)过程,通常表示为 \(u_t \sim A R C H(p)\) 。
下面我们以最简单的 \(\operatorname{ARCH}(1)\) 过程来说明,采用文献中惯用的方式可将 \(\operatorname{ARCH}(1)\) 过程表示为:
\[
\begin{aligned}
y_t & =\mathbf{x}_t^{\prime} \beta+u_t \\
u_t & =v_t \sqrt{h_t} \\
h_t & =a_0+a_1 u_{t-1}^2
\end{aligned}
\]
其中,\(v_t \sim \operatorname{IID} N(0,1), a_0>0\) 且 \(a_1<1\) 。则 \(u_t\) 的非条件期望和方差分别为:\({ }^1\)
\[
\begin{aligned}
\mathrm{E}\left(u_t\right) & =0 \\
\operatorname{Var}\left(u_t\right) & =\frac{a_0}{1-a_1}
\end{aligned}
\]
我们注意到,模型(11-3a)-(11-3c)完全满足传统线性回归模型的基本假设条件,因此,OLS 估计仍然是 \(\beta\) 的所有线性无偏估计中最有效的估计量 (BLUE)。
然而,由于模型具有 ARCH 效应,所以还存在更为有效的非线性估计量。 \(u_t\) 的条件期望和方差分别为:
\[
\begin{aligned}
\mathrm{E}\left(u_t \mid \Omega_{t-1}\right) & =0 \\
\operatorname{Var}\left(u_t \mid \Omega_{t-1}\right) & =\mathrm{E}\left(u_t^2 \mid \Omega_{t-1}\right) \\
& =a_0+a_1 u_{t-1}^2
\end{aligned}
\]
据此,我们可以进一步得到 \(y_t\) 的条件期望和条件方差:
\[
\begin{aligned}
\mathrm{E}\left(y_t \mid \Omega_{t-1}\right) & =\mathbf{x}_t^{\prime} \beta \\
\operatorname{Var}\left(y_t \mid \Omega_{t-1}\right) & =a_0+a_1 u_{t-1}^2
\end{aligned}
\]
因此,\(y_t\) 的条件方差同样是 \(u_{t-1}^2\) 的函数。换言之,ARCH 会直接影响干扰项 \(u_t\) ,而被解释变量 \(y_t\) 虽然是由线性模型产生,但由于其干扰项中包含了 ARCH 效应,所以 \(y_t\) 本身也是一个 ARCH 过程。
\(\operatorname{ARCH}(p)\) 模型及其扩展
前面已经提到,金融时间序列的波动往往具有"从聚性",因此将上面介绍的 \(\operatorname{ARCH}(1)\) 模型扩展至 \(\operatorname{ARCH}(\mathrm{p})\) 模型往往能够更好的描述这种波动特征。ARCH(p)模型可表示为:
\[
\begin{aligned}
u_t & =v_t \sqrt{h_t} \quad v_t \sim \operatorname{IID} N(0,1) \\
h_t & =a_0+a_1 u_{t-1}^2+a_2 u_{t-2}^2+\cdots+a_p u_{t-p}^2
\end{aligned}
\]
基于(14-1)的设定,我们可以把 \(\operatorname{ARCH}(p)\) 模型扩展为 \(\operatorname{AR}(m)-\operatorname{ARCH}(p)\) 模型:
\[
\begin{aligned}
y_t & =\delta+\sum_{j=1}^m \rho_j y_{t-j}+u_t \\
u_t & =v_t \sqrt{h_t} \quad v_t \sim \operatorname{IID} N(0,1) \\
h_t & =a_0+\sum_{j=1}^p a_j u_{t-j}^2
\end{aligned}
\]
显然,按照这一思路,我们同样可以建立 ARMA \((m, n)-\mathrm{ARCH}(p)\) 。 基于(14-3a)的设定,我们尚可把 \(\operatorname{ARCH}(p)\) 模型扩展为多元回归模型:
\[
\begin{aligned}
y_t & =\beta_0+\sum_{j=1}^k \beta_j x_{i t}+u_t \\
u_t & =v_t \sqrt{h_t} \quad v_t \sim \operatorname{IID} N(0,1) \\
h_t & =a_0+\sum_{j=1}^p a_j u_{t-j}^2
\end{aligned}
\]
这里,\(x_{i t}\) 为外生变量或被解释变量的滞后项。在金融时间序列分析中,如果研究的对象是资产价格,我们往往还会在模型设定中加入虚拟变量,以捕捉"周内川历效应"(day-of-the-week)。
例如,在分析股票价格的 1 资料时,我们便可以在(14-5a)的基础上作如下设定:
\[
y_t=\sum_{j=1}^k \beta_j x_{i t}+\sum_{l=1}^5 a_l D_{l t}+u_t
\]
其中,\(l=1\)(周一), 2 (周二), 3 (周三), 4 (周四), 5 (周五),\(D_{l t}\) 为 \(0 / 1\) 虚拟变量。
ARCH 效应的检验
在模型设定之前,我们需要检验是否存在 ARCH 或 GARCH 效应。前面已经提到,由于模型(14-3a)-(14-3b)的 OLS 估计是无偏且一致的,所以我们可以利用 OLS 估计的残差来检验 ARCH 效应是否存在。基本步骤如下:
第一步 采用 OLS 估计模型 \(y_t=\mathbf{x}_t^{\prime} \boldsymbol{\beta}+u_t\) ,得到残差 \(\hat{u}_t\) ,以及 \(\hat{u}_t^2\) ;
第二步 估计模型 \(\hat{u}_t^2=a_0+a_1 \hat{u}_{t-1}^2+\cdots+a_p \hat{u}_{t-p}^2\) ,得到 \(R^2\) ;
第三步 构造统计量:\(L M=T \cdot R^2 \sim \chi^2(p)\) 。
该检验山 Engle(1982)提出,基本思想在于,若不存在 ARCH 效应,则 \(\hat{a}_1, \hat{a}_2, \cdot, \hat{a}_p\) 应当不会显著异于零。因此,我们可以针对原假设 \(\mathrm{H}_0: a_1=a_2=\cdots=a_p=0\) 进行检验,并基于 LM原则构造统计量。
模型的评估
若我们设定的 ARCH 模型是正确的,那么标准化后的残差:
\[
z_t=\frac{u_t}{\sqrt{h_t}}
\]
应当为一 i.i.d 的随机序列。因此,我们可以通过分析序列 \(\left\{z_t\right\}\) 来评估模型的设定是否合理。具体而言,若均值方程设定无误,则 \(z_t\) 不应表现出显著的序列相关,这可以采用 Ljung-Box 统计量进行检验。我们可以采用同样的方法分析 \(z_t^2\) 以评判方差方程的设定情况。最后,通过分析 \(z_t\)的偏度、峰度以及分位-分位图(即,Q-Q 图),我们可以大体判定模型的分布假设是否合理。
GARCH 模型
GARCH 模型是对 ARCH 模型的扩展,允许条件方差不仅与过去的干扰项有关,还与过去的条件方差有关。GARCH 模型的基本形式为: \[
\begin{aligned}
u_t & =v_t \sqrt{h_t} \quad v_t \sim \operatorname{IID} N(0,1) \\
h_t & =a_0+\sum_{j=1}^p a_j u_{t-j}^2+\sum_{j=1}^q b_j h_{t-j}
\end{aligned}
\] 其中,\(a_0>0\),\(a_j \geq 0\),\(b_j \geq 0\)。显然,GARCH 模型的条件方差不仅与过去的干扰项有关,还与过去的条件方差有关。GARCH 模型的一个重要特征是其非条件方差是有限的,即: \[
Var(u_t) = \frac{a_0}{1 - \sum_{j=1}^p a_j - \sum_{j=1}^q b_j}
\] 其中,\(\sum_{j=1}^p a_j + \sum_{j=1}^q b_j < 1\)。这意味着 GARCH 模型可以捕捉到金融时间序列的波动性聚集现象。
GARCH 模型的一个重要应用是用于金融市场的风险管理。通过对 GARCH 模型的估计,我们可以得到未来的波动率预测,从而为投资者提供风险管理的依据。此外,GARCH 模型还可以用于资产定价、投资组合优化等领域。
GARCH 模型的估计通常采用最大似然估计(MLE)方法。由于 GARCH 模型的非线性特征,MLE 方法的计算相对复杂,通常需要使用数值优化算法来求解。
在实际应用中,GARCH 模型的参数估计和模型选择通常使用信息准则(如 AIC、BIC)来进行。信息准则可以帮助我们在不同的 GARCH 模型中选择最优模型,以便更好地拟合数据。 GARCH 模型的一个重要扩展是 EGARCH 模型(Exponential GARCH),它允许条件方差的对数为线性函数。EGARCH 模型可以更好地捕捉到金融时间序列中的非对称效应和杠杆效应。 EGARCH 模型的基本形式为: \[
\begin{aligned}
\log(h_t) & =a_0+\sum_{j=1}^p a_j \left(\frac{u_{t-j}}{\sqrt{h_{t-j}}}\right)^2+\sum_{j=1}^q b_j \log(h_{t-j})
\end{aligned}
\] 其中,\(a_0\) 是常数项,\(a_j\) 和 \(b_j\) 是模型参数。EGARCH 模型的一个重要特征是其条件方差的对数是线性函数,这使得 EGARCH 模型能够捕捉到金融时间序列中的非对称效应和杠杆效应。