ChatGPT: https://chatgpt.com/share/681a4ce7-41d8-8005-85c4-7bf9facd992a
无论任何模型都是对现实的简化,而这种简化的核心在于抓住事物的本质特征,然后使用合适的数学语言来描述它。
本讲会展示多种时序建模的思路,尝试刻画体重变化的规律。
大家最容易想到的就是线性模型,假设一个人的体重会随着时间的推移而逐渐增加,此时模型可以设定如下:
\[y_t = \beta_0 + \beta_1 t + \epsilon_t\]
这个模型的缺陷很明显:它假设体重变化是线性的,那么,如果 \(\beta_1\) 是正数,体重就会随着时间的推移而不断增加;如果 \(\beta_1\) 是负数,体重就会随着时间的推移而不断减少。
然而,现实中,很多人都有「身材管理」意识:通过调节饮食和锻炼,将自己的体重控制在一个合理的范围内。根据这个观察,我们可以设定一个具有「均值回复」特征的模型,此处的均值就是「目标体重」。例如,可以将模型设定如下:
\[y_t = \mu + \beta_1 (y_{t-1} - \mu) + \epsilon_t\]
这个模型的含义是,\(t\) 时点的体重由三部分构成:(1) 目标体重 \(\mu\);(2) 体重的调整 \(\beta_1 (y_{t-1} - \mu)\);(3) 随机因素 \(\varepsilon_{t}\)。
然而,现实中,想要将体重控制在一个合理的范围内,并非易事,除了要有意志力和自制力,还需要合理安排饮食和锻炼,而这些都是有成本的,即「调整成本」。基于这一观察,可以考虑使用部分调整模型来刻画体重的变化:
\[y_t - y_{t-1} = \lambda (y_t^* - y_{t-1}) + \epsilon_t\]
\(AR(p)\) 模型
在时间序列分析中,\(AR(p)\) 模型是最基本的模型之一。它假设当前值与过去 \(p\) 个时刻的值存在线性关系。一般形式为:
\[
X_t = \phi_1 X_{t-1} + phi_2 X_{t-2} + ... + \phi_p X_{t-p} + \epsilon_t \tag{1}
\]
其中,\(\phi_1, \phi_2, ..., \phi_p\) 是模型参数,\(\epsilon_t\) 是白噪声项。
\(AR(1)\) 模型
当 \(p=1\) 时,\(AR(1)\) 模型为:
\[
X_t = \phi_1 X_{t-1} + \epsilon_t \tag{2}
\]
虽然看起来很简单,但 \(AR(1)\) 模型在时间序列分析中非常重要,因为它可以捕捉到数据的自相关性。从模型设定形式上来看,它具有递推的特征,当前值仅与前一个值相关。
具体而言,(2) 式在 \(t-1\) 时刻可以表示为:
\[
X_{t-1} = \phi_1 X_{t-2} + \epsilon_{t-1} \tag{3}
\]
将 (3) 式代入 (2) 式中,我们可以得到:
\[
X_t = \phi_1 (\phi_1 X_{t-2} + \epsilon_{t-1}) + \epsilon_t = \phi_1^2 X_{t-2} + \phi_1 \epsilon_{t-1} + \epsilon_t \tag{4}
\]
将 (4) 式继续递推下去,我们可以得到:
\[
X_t = \phi_1^t X_0 + \sum_{i=0}^{t-1} \phi_1^i \epsilon_{t-i} \tag{5}
\]
由 (5) 式可知,\(X_t\) 由初始值 \(X_0\) 和过去的随机扰动项 \(\epsilon_{t-i}\) 线性组合而成。
举个例子:若 \(X_0\) 表示某人 20 岁时的体重,取 \(t = 10\),则 \(X_{10}\) 表示该人 30 岁时的体重。假设 \(X_0 = 60 kg\),\(\phi_1 = 0.9\),则 (5) 式的含义是:
- 该人 30 岁时的体重 \(X_{10}\),由其 20 岁时的体重 \(X_0\) 与过去 10 年中的随机扰动项 \(\varepsilon_{t-i}\)(如饮食习惯、运动频率、作息变化、疾病史等)线性加权而成。
- 由于 \(\phi_1 = 0.9\),而 \(\phi_1^{10} = 0.9^{10} \approx 0.35\),说明 20 岁时的初始体重对 30 岁时体重的影响仍然存在,但已显著减弱。体重的变化更多地取决于过去 10 年逐年积累的生活方式等随机因素。
- 模型还体现出“记忆衰减”效应:越接近当前年份的扰动项,其影响越大。例如,\(\varepsilon_9\) 的系数为 \(\phi_1^1 = 0.9\),\(\varepsilon_8\) 的系数为 \(\phi_1^2 = 0.81\),\(\varepsilon_7\) 的系数为 \(\phi_1^3 \approx 0.729\),依此类推,扰动项的影响呈指数递减。
\(AR(1)\) 过程的平稳性
\(AR(1)\) 过程的平稳性是指时间序列的均值、方差和自协方差不随时间变化。对于 \(AR(1)\) 模型,平稳性条件为: \[|\phi_1|<1\]
下面,我们来模拟生成几组 \(AR(1)\) 过程的数据。
请思考如下几个问题: - \(AR(1)\) 模型能刻画一个人的体重变化吗? - 不同的 \(\phi_1\) 对数据生成有何影响? - 模拟过程中,假设 \(\epsilon_t \sim (0, \sigma^2)\),参数 \(\sigma\) 的取值对数据生成有何影响? - 如何修改这个模型才能更好地刻画一个人的体重变化?
import numpy as np
import matplotlib.pyplot as plt
# 参数设置
phi_1 = 0.99 # AR(1) 系数
sigma = 5 # 随机扰动项的标准差
X_0 = 60 # 初始体重 (kg)
n_years = 10 # 模拟 10 年
n_steps = n_years * 12 # 每年 12 个月
# 随机扰动项 (白噪声)
np.random.seed(1234) # 固定随机种子以便复现
epsilon = np.random.normal(loc=0, scale=sigma, size=n_steps)
# 模拟 AR(1) 过程
X = np.zeros(n_steps)
X[0] = X_0
for t in range(1, n_steps):
X[t] = phi_1 * X[t-1] + epsilon[t]
# 绘图
time = np.arange(1, n_steps + 1) / 12 # 时间轴 (以年为单位)
plt.figure(figsize=(12, 6))
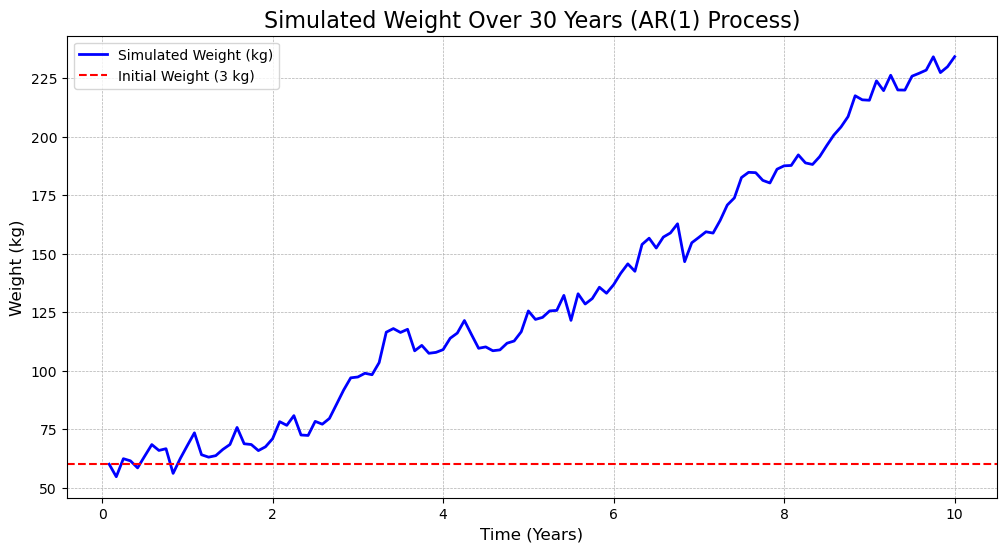
plt.plot(time, X, label="Simulated Weight (kg)", color="blue", linewidth=2)
plt.axhline(y=X_0, color="red", linestyle="--", label="Initial Weight (3 kg)")
plt.title("Simulated Weight Over 30 Years (AR(1) Process)", fontsize=16)
plt.xlabel("Time (Years)", fontsize=12)
plt.ylabel("Weight (kg)", fontsize=12)
plt.legend()
plt.grid(True, linestyle="--", linewidth=0.5)
plt.show()
分析: - \(AR(1)\) 过程的期望值是常数,
带时间趋势项的 \(AR(1)\) 模型
- \(AR(1)\) 过程的方差是常数,且与 \(\phi_1\) 无关
- \(AR(1)\) 过程的自协方差是常数,且与 \(\phi_1\) 无关
简单的 \(AR(1)\) 模型无法刻画一个人的体重变化,因为它的均值和方差都是常数,且自协方差也是常数。 - 体重变化是一个非平稳的过程,均值和方差都随时间变化。 - 体重变化受多种因素影响,如饮食、运动、生活习惯等,不能仅用一个参数来描述。 - 体重变化具有一定的趋势性,如随着年龄增长,体重可能会增加或减少。
因此,我们需要引入时间趋势项来改进模型,基本模型设定形式如下:
\[X_t = \phi_1 X_{t-1} + \beta t + \epsilon_t \tag{6}\]
其中,\(\beta\) 是时间趋势项的系数,\(t\) 是时间变量。
- 式中,\(\beta t\) 表示随着时间的推移,体重会有一个线性变化趋势。
当 \(\beta > 0\) 时,表示体重随时间增加;
当 \(\beta < 0\) 时,表示体重随时间减少;
当 \(\beta = 0\) 时,表示体重没有明显的线性变化趋势。
该模型仍然具有递推的特征,当前值与前一个值相关,但同时考虑了时间趋势项的影响。
该模型仍然具有记忆衰减效应,当前值与前一个值的关系更强,随着时间的推移,影响逐渐减弱。
# 带有时间趋势项的 AR(1) 模型 (每年 12 个月)
# 参数设置
phi_1 = 0.96 # AR(1) 系数
sigma = 2 # 随机扰动项的标准差
X_0 = 60 # 初始体重 (kg)
n_years = 10 # 模拟 10 年
n_steps = n_years * 12 # 每年 12 个月
t = np.arange(1, n_steps + 1) / 12 # 时间轴 (以年为单位)
beta = 0.5 # 时间趋势项的系数
# 随机扰动项 (白噪声)
np.random.seed(12345) # 固定随机种子以便复现
epsilon = np.random.normal(loc=0, scale=sigma, size=n_steps)
# 模拟带时间趋势项的 AR(1) 过程
X = np.zeros(n_steps)
X[0] = X_0
for i in range(1, n_steps):
X[i] = phi_1 * X[i-1] + beta * t[i] + epsilon[i]
# 绘图
plt.figure(figsize=(12, 6))
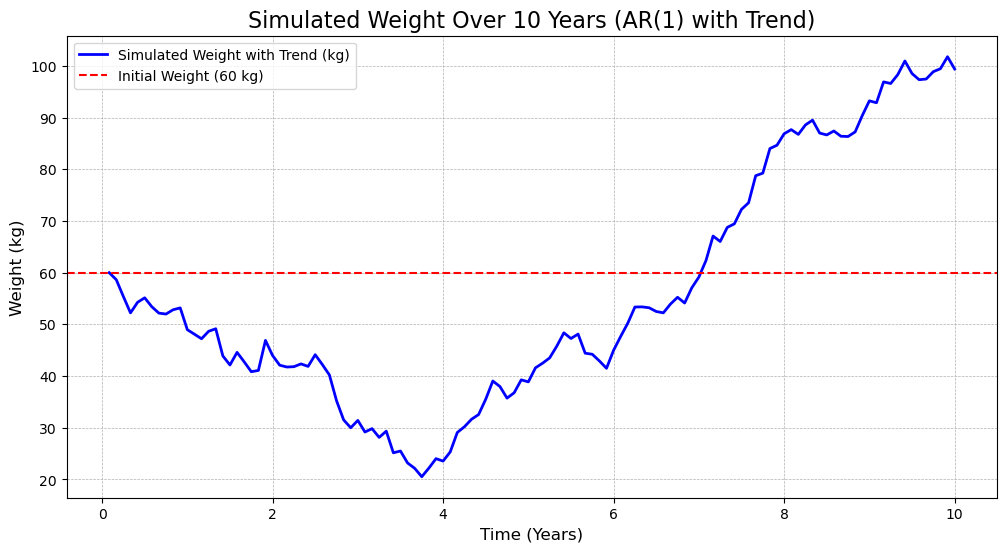
plt.plot(t, X, label="Simulated Weight with Trend (kg)", color="blue", linewidth=2)
plt.axhline(y=X_0, color="red", linestyle="--", label=f"Initial Weight ({X_0} kg)")
plt.title(f"Simulated Weight Over {n_years} Years (AR(1) with Trend)", fontsize=16)
plt.xlabel("Time (Years)", fontsize=12)
plt.ylabel("Weight (kg)", fontsize=12)
plt.legend()
plt.grid(True, linestyle="--", linewidth=0.5)
plt.show()
你的代码确实在数学上是一个标准的 AR(1) 过程模拟,但将其用于模拟“体重”这一现实变量时,会出现明显不合理的结果,比如长期内可能体重变得极大或极小,甚至负数。根本原因在于:
- AR(1) 是线性过程,没有任何边界或长期均值约束,不能自然模拟体重这种具有生理限制、趋势和波动特征的变量;
- 模拟过程中初始值为 3kg,这可能适合婴儿,但无法解释成人体重发展过程;
- 扰动项是对称的正态分布,容易导致极端情况。
更合理的模拟方式
1. 引入趋势项 + 均值回复项(趋势 + OU过程)
现实中,体重会随着年龄增长逐渐上升,然后趋于稳定,有轻微波动。这可以用如下模型:
\[
W_t = \mu + \theta (W_{t-1} - \mu) + \varepsilon_t
\]
其中:
- \(\mu\) 是目标体重水平(如 70kg);
- \(\theta\) 控制恢复速度(\(0 < \theta < 1\));
- \(\varepsilon_t \sim N(0, \sigma^2)\)
这称为 Ornstein–Uhlenbeck (OU) 过程的离散版本。
# 改进的模拟代码(成年人体重演化)
import numpy as np
import matplotlib.pyplot as plt
# 设置参数
mu = 70 # 长期均衡体重 (kg)
theta = 0.95 # 回复速度 (0<theta<1,越小回复越快)
sigma = 1.5 # 扰动项标准差
W_0 = 50 # 初始体重 (kg)
n_years = 10
n_steps = n_years * 12
# 白噪声扰动项
np.random.seed(123)
epsilon = np.random.normal(0, sigma, n_steps)
# 模拟 OU 过程
W = np.zeros(n_steps)
W[0] = W_0
for t in range(1, n_steps):
W[t] = mu + theta * (W[t-1] - mu) + epsilon[t]
# 绘图
time = np.arange(1, n_steps + 1) / 12
plt.figure(figsize=(12, 6))
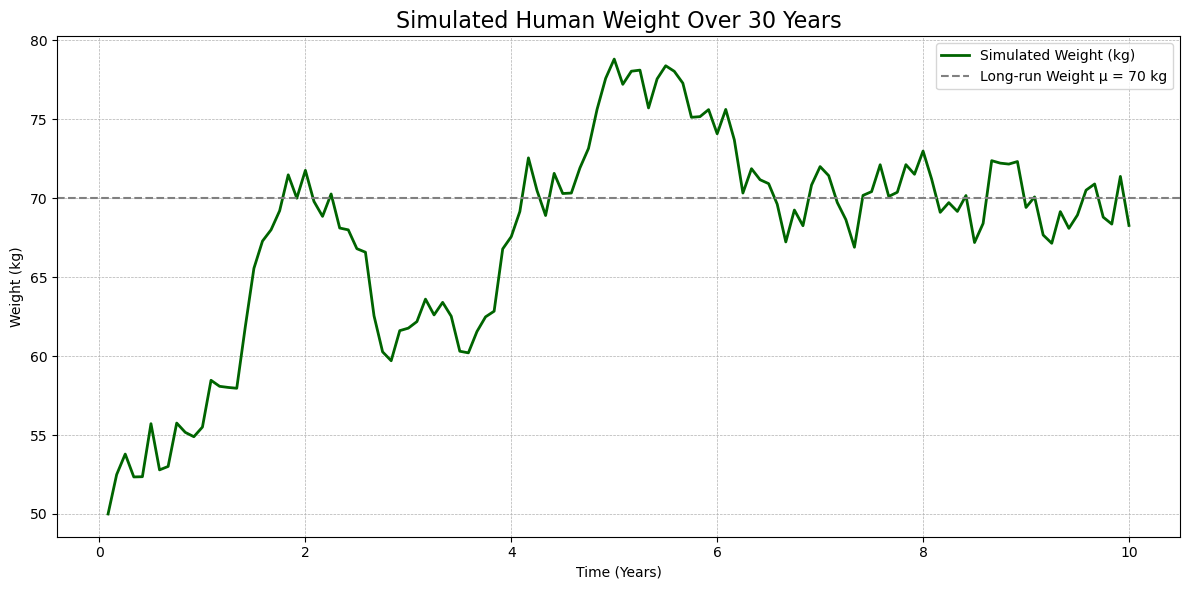
plt.plot(time, W, label="Simulated Weight (kg)", color="darkgreen", linewidth=2)
plt.axhline(mu, color="gray", linestyle="--", label=f"Long-run Weight μ = {mu} kg")
plt.title("Simulated Human Weight Over 30 Years", fontsize=16)
plt.xlabel("Time (Years)")
plt.ylabel("Weight (kg)")
plt.grid(True, linestyle="--", linewidth=0.5)
plt.legend()
plt.tight_layout()
plt.show()
3. 进一步改进建议
- 若模拟儿童成长,可引入 非线性增长趋势(如 logistic 或 spline);
- 若模拟节食、锻炼干预等,可引入 断点 或 政策冲击项;
- 若模拟个体差异,可引入 随机效应项 或分组参数。
儿童体重的 Logistic 增长模型
Logistic 函数形式如下:
\[
W_t = \frac{W_{\max}}{1 + \exp(-k(t - t_0))} + \varepsilon_t
\]
以下是你那段内容的正确公式格式修订版本,符合你指定的写作规范:
- \(W_{max}\):成年期体重极限值(如 65 kg)
- \(k\):增长速率(如 0.4)
- \(t_0\):拐点(体重增长最快的时间点,单位为年)
- \(ϵ_t\):扰动项(模拟个体差异或偶发波动)
## 示例代码:儿童成长过程中的体重变化
import numpy as np
import matplotlib.pyplot as plt
# 模拟参数
W_max = 65 # 成年体重上限 (kg)
k = 0.4 # 增长速度
t0 = 12 # 拐点年龄(增长最快期)
sigma = 0.5 # 扰动标准差
n_years = 22
n_steps = n_years * 12
t = np.arange(n_steps) / 12 # 时间轴(以年为单位)
# 随机扰动项(模拟月度波动)
np.random.seed(42)
epsilon = np.random.normal(0, sigma, size=n_steps)
# Logistic 增长体重
W = W_max / (1 + np.exp(-k * (t - t0))) + epsilon
# 绘图
plt.figure(figsize=(12, 6))
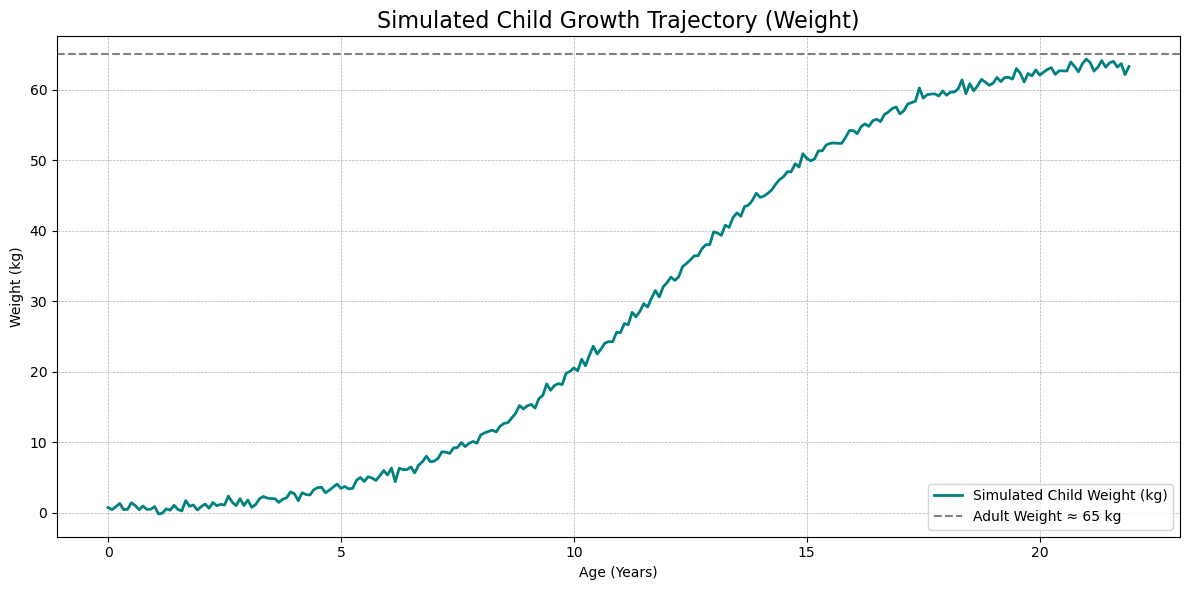
plt.plot(t, W, label="Simulated Child Weight (kg)", color="teal", linewidth=2)
plt.axhline(W_max, linestyle="--", color="gray", label=f"Adult Weight ≈ {W_max} kg")
plt.title("Simulated Child Growth Trajectory (Weight)", fontsize=16)
plt.xlabel("Age (Years)")
plt.ylabel("Weight (kg)")
plt.legend()
plt.grid(True, linestyle="--", linewidth=0.5)
plt.tight_layout()
plt.show()
结果特性说明
- 出生阶段体重较低;
- 在 \(t_0\) 附近(如青春期前后)增长最快;
- 接近成年后体重趋于稳定在 \(W_{max}\) 附近;
- 加入扰动项 \(varepsilon_t\),体现不同孩子之间的个体差异。
三段式样条(piecewise spline)函数模型
以下是一个 三段式样条(piecewise spline)函数模型,用于模拟儿童体重的非线性增长轨迹,具有更灵活的形状变化,适合描述 婴幼儿期缓慢增长 → 少年期快速增长 → 成年期稳定 的过程。
模型设定:三段线性 spline(断点在 \(t_1=5\) 岁和 \(t_2=12\) 岁)
\[
W_t = \beta_0 + \beta_1 t + \beta_2 (t - t_1)_+ + \beta_3 (t - t_2)_+ + ϵ_t
\]
其中:
- \((x)_+ = \max(0, x)\) 表示正部函数,用于确保断点后的增长速率仅在超过断点时生效。例如,当 \(t < t_1\) 时,\((t - t_1)_+ = 0\),表示断点 \(t_1\) 对体重增长没有影响;当 \(t \geq t_1\) 时,\((t - t_1)_+ = t - t_1\),表示断点 \(t_1\) 开始对体重增长产生作用。
- \(\beta_0\) 是基准体重;
- \(\beta_1\) 是婴幼儿期增长速度;
- \(\beta_2\) 是 5 岁以后增长速度的变动;
- \(\beta_3\) 是 12 岁以后增长速度的变动;
- \(ϵ_t\) 是扰动项,模拟波动与个体差异。
用 Indicator Function 表达模型
上述三段式样条模型可以用 Indicator Function 表达为:
\[
W_t = \beta_0 + \beta_1 t + \beta_2 \cdot \mathbb{1}(t > t_1) \cdot (t - t_1) + \beta_3 \cdot \mathbb{1}(t > t_2) \cdot (t - t_2) + \epsilon_t
\]
其中:
- \(\mathbb{1}(\cdot)\) 是 Indicator Function,当条件为真时取值为 1,否则为 0;
- \(\beta_0\) 是初始体重;
- \(\beta_1\) 是婴幼儿期的增长速率;
- \(\beta_2\) 和 \(\beta_3\) 分别表示在断点 \(t_1\) 和 \(t_2\) 之后的增长速率变化;
- \(\epsilon_t\) 是随机扰动项,模拟个体差异或偶发波动。
模型解释
- 分段增长:
- 在 \(t \leq t_1\) 时,\(W_t = \beta_0 + \beta_1 t + \epsilon_t\),表示婴幼儿期的线性增长;
- 在 \(t_1 < t \leq t_2\) 时,\(W_t = \beta_0 + \beta_1 t + \beta_2 (t - t_1) + \epsilon_t\),表示少年期增长速率的变化;
- 在 \(t > t_2\) 时,\(W_t = \beta_0 + \beta_1 t + \beta_2 (t - t_1) + \beta_3 (t - t_2) + \epsilon_t\),表示成年期增长速率的进一步变化。
- 灵活性:
- 通过引入断点 \(t_1\) 和 \(t_2\),模型能够捕捉体重增长的非线性特征;
- 不同阶段的增长速率可以通过 \(\beta_1, \beta_2, \beta_3\) 灵活调整。
- 现实意义:
- 该模型适合描述儿童体重的增长轨迹,能够反映婴幼儿期缓慢增长、少年期快速增长、成年期趋于稳定的过程。
边际效应
边际效应是指在给定的自变量水平下,因变量对自变量的变化率。对于三段式样条模型,可以通过求导来计算边际效应 \(\frac{\partial{y}}{\partial{t}}\): - 在 \(t \leq t_1\) 时,边际效应为 \(\frac{\partial{y}}{\partial{t}} \mid_{t \leq t_1}= \beta_1\);
- 在 \(t_1 < t \leq t_2\) 时,边际效应为 \(\frac{\partial{y}}{\partial{t}} \mid_{t_1 < t \leq t_2} = \beta_1 + \beta_2\);
- 在 \(t > t_2\) 时,边际效应为 \(\frac{\partial{y}}{\partial{t}} \mid _{t > t_2} = \beta_1 + \beta_2 + \beta_3\)。
## Python 实现代码
import numpy as np
import matplotlib.pyplot as plt
# 时间设定
n_years = 18
n_steps = n_years * 12
t = np.arange(n_steps) / 12 # 年龄(以年为单位)
# 断点设定
t1 = 5
t2 = 12
# Spline 变量
def positive_part(x):
return np.maximum(0, x)
s1 = positive_part(t - t1)
s2 = positive_part(t - t2)
# 模拟参数
beta_0 = 3 # 初始体重(kg)
beta_1 = 1.5 # 0-5 岁期间增长速率
beta_2 = 2.0 # 5-12 岁之后的增长变化
beta_3 = -1.2 # 12 岁之后的增长放缓
sigma = 0.8 # 扰动标准差
# 随机扰动项
np.random.seed(42)
epsilon = np.random.normal(0, sigma, size=n_steps)
# 构建体重轨迹
W = beta_0 + beta_1 * t + beta_2 * s1 + beta_3 * s2 + epsilon
# 绘图
plt.figure(figsize=(12, 6))
plt.plot(t, W, label="Simulated Weight (Piecewise Spline)", color="purple", linewidth=2)
plt.axvline(x=t1, linestyle="--", color="gray", label=f"Breakpoint: {t1} years")
plt.axvline(x=t2, linestyle="--", color="gray", label=f"Breakpoint: {t2} years")
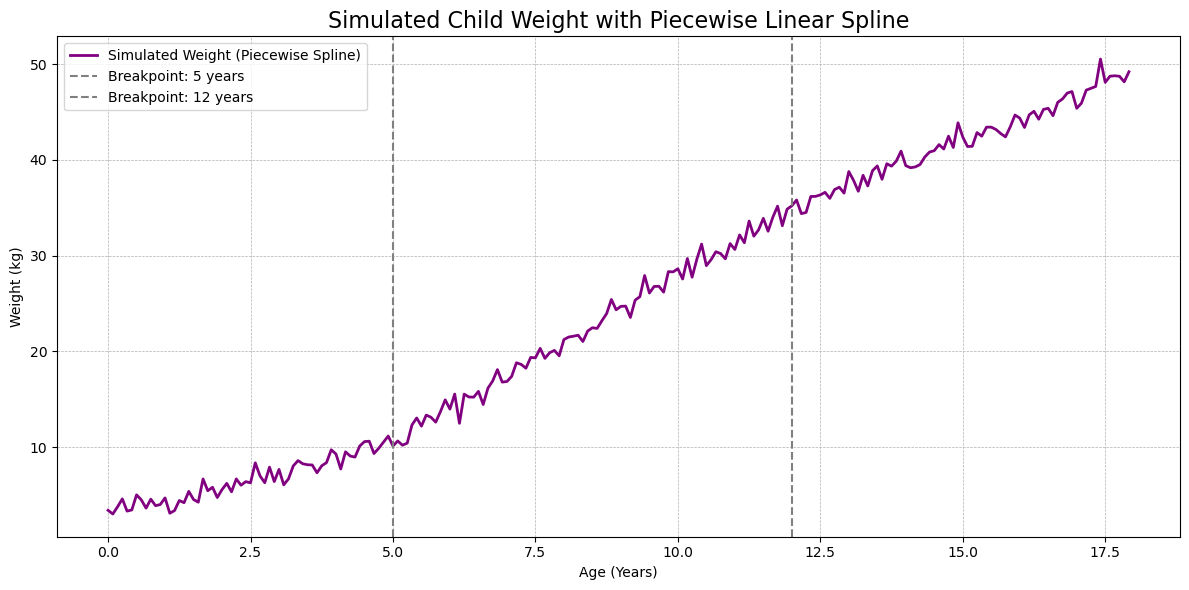
plt.title("Simulated Child Weight with Piecewise Linear Spline", fontsize=16)
plt.xlabel("Age (Years)")
plt.ylabel("Weight (kg)")
plt.grid(True, linestyle="--", linewidth=0.5)
plt.legend()
plt.tight_layout()
plt.show()
需要我继续输出自然样条(cubic spline)或用 patsy 和 statsmodels 等 Python 包自动拟合的版本吗?