import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# 固定随机数种子,确保结果可复现
np.random.seed(42)
# 假定实验组与对照组各 500 人
n_A, n_B = 500, 500
# 设定两组消费金额均值和标准差(单位:元)
mean_A, std_A = 38, 8
mean_B, std_B = 41, 9
# 生成两组消费金额数据(正态分布)
amount_A = np.random.normal(loc=mean_A, scale=std_A, size=n_A)
amount_B = np.random.normal(loc=mean_B, scale=std_B, size=n_B)
# 组装数据为 DataFrame
df = pd.DataFrame({
'amount': np.concatenate([amount_A, amount_B]),
'group': ['A']*n_A + ['B']*n_B
})28 A/B test-分组对照试验
- 案例 1:A/B 检验:新版网页更有吸引力吗?
- 案例 2:A/B 检验:支付宝营销策略效果分析
28.1 简介
近年来,金融科技公司不断尝试提升贷款客户的还款率。例如,「某金融公司」通过数据分析发现,许多客户因遗忘或忽视账单信息而逾期。市场与风控团队提出:如果在还款日前定时发送短信提醒,能否显著提升客户的按时还款率?
在全面推行这个新策略之前,公司希望通过科学方法验证其有效性。目前的验证方法有如下几种:
- 用户调查:通过问卷了解客户对短信提醒的态度。
- 历史数据分析:随即挑选 1000 名客户,对他们实施新的策略——「短信提醒」,分析他们在新旧两种策略下的还款率差异。
- A/B 测试:将客户随机分为两组,一组接受短信提醒,另一组不接受,比较两组的还款率差异。
讨论:上述三种方法的优点和缺点是什么?
28.1.1 什么是 A/B 测试?
A/B 测试,也被称为分组对照实验(Randomized Controlled Trial, RCT),是数据分析和产品优化领域中常用的一种实验设计方法。A/B 测试通过将用户或样本随机分为两组——实验组 (B 组) 和对照组 (A 组),并分别施加不同的处理或策略,比较两组关键指标的差异,从而评估某项新方案或改进措施是否有效。
应用场景举例:
- 电商平台测试新页面设计是否提升转化率
- 金融公司测试短信提醒是否提升客户还款率
- 餐饮店「直接打折」v.s.「赠送现金券」的促销效果
A/B 测试以其操作简单、原理严谨、结果直观的特点,被广泛应用于互联网、零售、金融等行业的数据驱动决策流程中。
28.1.2 A/B 测试的基本流程
- 明确实验目标:如提升转化率、点击率或收入
- 确定实验组与对照组:通常采用随机分组,保证组间差异仅来源于处理
- 实施实验:对实验组应用新策略,对照组保持原有方案
- 收集数据:追踪并记录各组的核心指标
- 统计检验:比较两组指标的显著性差异
- 结果分析与决策:判断新策略是否优于原方案
28.2 案例引入与问题设定
28.2.1 案例背景:咖啡店促销策略优化
假设你在某连锁咖啡品牌的运营团队工作。近期,为了提升门店销量,市场部设计了两种不同的促销方案:
- A 方案(对照组):原有满 30 元减 5 元活动
- B 方案(实验组):满 40 元减 10 元活动
日常运营中,人们常常认为加大折扣就一定能带来更高消费,但实际效果却受到多种因素影响。只有通过随机分组实验和统计检验,才能避免偶然性和主观偏差,客观评估新策略的价值。
为此,门店计划进行为期一个月的测试,在此期间,将顾客随机分为两组,分别接受 A 或 B 方案。管理层希望通过 A/B 测试,判断哪种方案能更有效地提升人均消费金额。
28.2.2 指标设定与分析思路
核心指标:人均消费金额
数据需求:每位顾客的消费金额、所属促销组别
分析思路:
- 对比两组顾客的人均消费金额
- 采用 t 检验或非参数检验判断差异是否显著
- 对结果进行业务解读,提出运营建议
28.3 随机分组与实验控制
A/B 测试的关键在于科学分组。随机分组意味着每一个样本都被赋予相同的概率进入实验组或对照组,从而最大程度上消除两组间的系统性差异,使实验结果具有因果解释力。
28.3.1 如何实现随机分组?
在业务系统中,常见做法有按照用户 ID 尾号、系统随机数等方式分配用户,也可以利用 Python 中的 numpy 包提供的随机抽样函数直接实现。
下面是 Python 的实现方式示例:
28.3.2 分层随机分组
分层随机分组(Stratified Randomization)是指先将样本按某些关键特征分层,然后在每一层内进行独立的随机分组,以保证组间关键变量的分布均衡。
实践建议:分层变量可以是性别、年龄段、会员等级、地域等类别变量。在如下几种情况下,建议使用分层随机分组:
- 当核心指标受某些特征影响较大时 (如短信提醒对不同年龄段的客户效果不同),如果完全随机分组,容易导致这些特征在两组间分布不均,影响实验结果的解释性。
- 当样本量较小,且样本在各个组别中的分布很不均匀时,分层随机分组可以保证各组抽样的代表性 (抽样的相对比例保持一致)
Python 实现举例:
28.4 核心指标及多指标综合评价
A/B 测试的成败,很大程度上取决于你设定的评价指标。不同业务场景会选取不同的核心指标。常见的指标如下:
转化率(Conversion Rate):完成特定目标(如下单、注册、付费)的用户比例。
\[ \text{转化率} = \frac{\text{转化用户数}}{\text{总用户数}} \]
点击率(Click Through Rate, CTR):广告、页面等在一段时间内被点击次数占总展示次数的比例。
\[ \text{点击率} = \frac{\text{点击次数}}{\text{展示次数}} \]
复购率(Repeat Purchase Rate):在指定时期内,发生过多次购买的用户比例。
\[ \text{复购率} = \frac{\text{多次购买用户数}}{\text{总用户数}} \]
多指标综合评价
在实际分析中,通常不会只看一个指标。例如,电商会同时关注点击率、转化率、客单价、利润率等多个指标。因为,有些政策或策略虽然在某个指标上收效良好,但却可能对其他指标产生负面影响,反之亦然。
需要注意的是,当同时关注多个指标时,要注意多重检验问题,即检验的指标越多,“误判为有效”的概率也会上升。常用如 Bonferroni 修正 等方法,调整各项检验的显著性水平,降低假阳性的概率。
28.5 统计检验方法详解
28.5.1 均值差异的 t 检验(独立样本 t 检验)
适用场景:对照组和实验组数据近似正态分布,且样本独立。
检验原理:对比两组均值,判断其差异是否显著。
假设:
\[ H_0: \mu_A = \mu_B \quad v.s. \quad H_1: \mu_A \neq \mu_B \]
同方差时,用 Student’s t 检验:
\[ t = \frac{\bar{x}_A - \bar{x}_B}{\sqrt{s_p^2\left(\frac{1}{n_A} + \frac{1}{n_B}\right)}} \]
其中,
\[ s_p^2 = \frac{(n_A - 1)s_A^2 + (n_B - 1)s_B^2}{n_A + n_B - 2} \]
\(\bar{x}_A, \bar{x}_B\):对照组与实验组均值
\(s_A^2, s_B^2\):两组的样本方差
\(n_A, n_B\):两组的样本容量
存在异方差时,用 Welch 检验:
\[ t = \frac{\bar{x}_A - \bar{x}_B}{\sqrt{\frac{s_A^2}{n_A} + \frac{s_B^2}{n_B}}} \]
自由度采用 Satterthwaite 近似法计算。详见:Welch’s t-test (Wikipedia)。
Python 代码为:
28.5.2 非参数检验(Mann-Whitney U 检验)
适用场景:当样本分布偏态或存在异常值时,采用非参数检验方法更稳健。
检验原理:将两组样本混合排序,比较每组的秩和,判断分布是否有统计显著差异。
U 统计量计算公式:
\[ U_A = n_A n_B + \frac{n_A(n_A+1)}{2} - R_A \]
其中,\(R_A\) 为对照组所有样本的秩次之和,\(n_A\)、\(n_B\) 分别为组容量。详情参见:Mann-Whitney U test (Wikipedia)。
Python 代码为:
28.5.3 转化率/比例的 Z 检验
适用场景:核心指标为转化率等比例变量时
原假设:两组转化率无显著差异
统计量:
\[ Z = \frac{p_A - p_B}{\sqrt{p(1-p)\left(\frac{1}{n_A} + \frac{1}{n_B}\right)}} \]
其中,
\[ p = \frac{n_A p_A + n_B p_B}{n_A + n_B} \]
\(p_A, p_B\):两组的转化率
原理说明:Z 检验通过构建标准正态分布下的比较区间,评估比例差异是否显著。
python 代码为:
28.5.4 显著性水平、P 值
显著性水平(Significance Level, \(\alpha\))
- 显著性水平 \(\alpha\) 通常设为 0.05,表示我们允许有 5% 的概率把本来无差异的组误判为有差异(即“假阳性”)。
- 在实际分析中,根据业务容忍度可以取 0.01、0.05 或 0.10。
P 值(P-value):P 值(P-value)是统计推断中判断实验结果是否显著的关键指标。
- 从专业角度看,P 值表示:在原假设(比如短信提醒没有效果)成立的前提下,观察到当前结果或更极端结果的概率。如果 P 值很小(通常小于 0.05),说明在原假设为真的情况下,我们现在看到的数据几乎很难靠偶然性解释,这就为我们拒绝原假设提供了统计证据。
- 通俗来讲,P 值越小,表示实验组和对照组之间出现如此大差异“纯属巧合”的可能性越低,因此我们更有理由相信新措施(如短信提醒)确实产生了效果。
- 但要注意,P 值只是‘差异是否偶然’的统计证据,具体业务决策还要结合实际背景综合判断。**
28.5.5 置信区间
点估计与区间估计
在 A/B 测试等数据分析中,估计出的 A 组和 B 组的平均差异 \(d = \bar{x}_A - \bar{x}_B\) 称为「点估计」。由于它是一个随机变量,单纯看 \(d\) 的数值是没有意义的,需要根据其标准误来构造 t 统计量来执行假设检验。
另一种常用的估计方法是区间估计,它提供了一个范围而不是单一数值。我们常用置信区间(Confidence Interval, CI)来表达对总体参数(如均值、比例等)的不确定性估计。例如,我们估算短信提醒提升还款率,得到「提升幅度的 95% 置信区间为 \([2\%, 5\%]\)」。
置信区间的含义
- 置信区间是一种区间估计方法,在一定置信度(比如 95%)下,为总体参数提供一个可能的取值范围。
- 「95%」的本质含义是如果我们在同样条件下反复采样并计算置信区间,理论上有 95% 的区间会覆盖真实参数值。
具体解释如下:
如果用同样的估计方法重复很多次实验 (如 \(K=1000\) 次),每次都计算一个区间 \(R_k = [L_k, U_k]\),其中 \(L_k\) 和 \(U_k\) 分别是下限和上限。最终会得到 1000 个区间估计,记为 \(\{R_1, R_2, \ldots, R_K\}\)。那么,理论上,在这 1000 个置信区间中,约有 950 个 (占比约为 \(0.95\)) 会包含真实参数 \(\mu\)。
我们平时所说的「95% 的覆盖率」,指的便是这种多次实验的总体结果。
单次置信区间的含义
在实际分析中,我们往往只进行一次实验,也只能计算出一个置信区间(如 \([2\%, 5\%]\))。对于这一次计算出的区间,真实参数要么在区间内,要么不在区间内。我们不能说“参数有 95% 的概率落在本次区间内” (这是一种非常普遍的错误理解)。我们只能说,\([2\%, 5\%]\) 有「95% 的可靠性」或「95% 的覆盖率」。
28.6 样本量与实验效能
样本量不足可能导致“假阴性”(即实际上存在差异,但没有检验出来)。虽然通常来讲,样本量越大,检验的统计效能越高,但过大的样本量会导致资源浪费和计算效率低下。因此,在设计 A/B 测试时,需要合理计算所需的样本量。
功效分析(Power Analysis) 用于预先计算所需样本量,以保证检验的敏感性和可靠性。
样本量计算公式(以均值差异检验为例):
\[ n = \left(\frac{(Z_{\alpha/2} + Z_{\beta}) \cdot (s_A + s_B)}{d}\right)^2 \]
其中:
\(Z_{\alpha/2}\):显著性水平对应的 Z 值
\(Z_{\beta}\):检验功效对应的 Z 值
\(s_A, s_B\):两组样本的标准差
\(d\):期望的最小效应的大小(即两组均值差异)
Python 实现:
28.7 Python 实操:咖啡店促销方案
本节将以「咖啡店促销方案」为例,完整展示 A/B 测试的数据生成、分组、统计检验和结果可视化的全过程。所有代码均配详细中文注释,便于初学者自学和复现。
28.7.1 数据背景与问题回顾
业务场景简述
某连锁咖啡店运营团队为了提升门店人均消费金额,设计了两种促销方案:
- A 方案(对照组):满 30 元减 5 元
- B 方案(实验组):满 40 元减 10 元
运营团队在 1000 名顾客中随机分配上述两种方案,希望评估「B 方案」是否能显著提升人均消费。
分析目标
- 检验实验组和对照组人均消费金额是否有统计学上的显著差异
- 提供业务解读与决策建议
28.7.2 数据模拟与分组
28.7.3 数据可视化与描述统计
28.7.3.1 描述统计
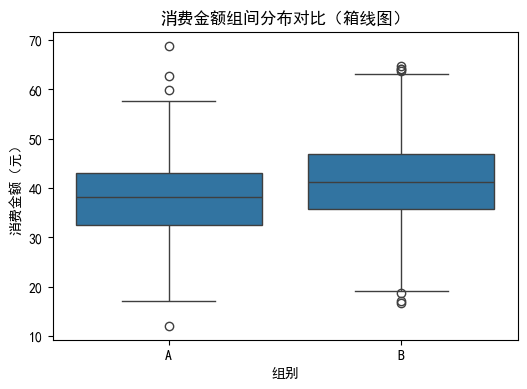
28.7.3.2 2. 消费金额分布对比
# 绘制实验组与对照组的消费金额密度函数图
plt.figure(figsize=(8, 5))
sns.kdeplot(amount_A, label='Group A', color='blue', fill=True, alpha=0.3)
sns.kdeplot(amount_B, label='Group B', color='orange', fill=True, alpha=0.3)
plt.title('Density Plot of Amount by Group')
plt.xlabel('Amount (RMB)')
plt.ylabel('Density')
plt.legend(title='Group')
plt.grid(alpha=0.2)
# 注释:两组的消费金额分布密度对比
plt.show()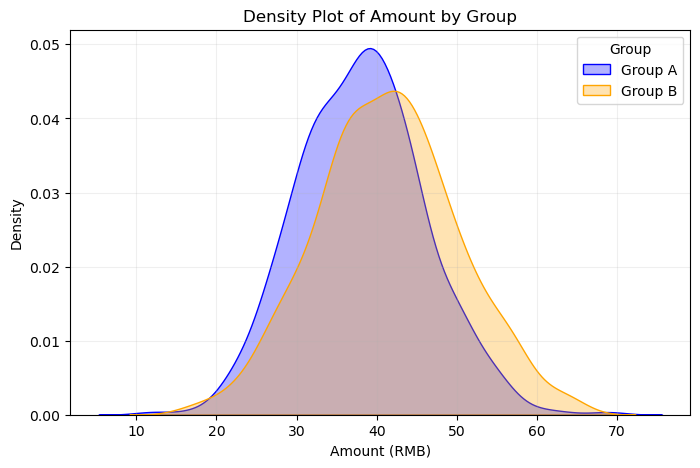
28.7.3.3 3. 箱线图
28.7.4 统计检验
28.7.4.1 独立样本 t 检验
from scipy.stats import ttest_ind
# 拆分两组数据
amount_A = df[df['group'] == 'A']['amount']
amount_B = df[df['group'] == 'B']['amount']
# 检验方差齐性
from scipy.stats import levene
stat_levene, p_levene = levene(amount_A, amount_B)
print(f'Levene 检验 P 值:{p_levene:.4f}')
# 执行 t 检验(自动检测方差是否齐性)
equal_var = p_levene > 0.05
t_stat, p_value = ttest_ind(amount_A, amount_B,
equal_var=equal_var)
print(f't 检验 P 值:{p_value:.4f}')Levene 检验 P 值:0.0146
t 检验 P 值:0.000028.7.4.2 Mann-Whitney U 检验(非参数)
28.7.5 功效分析
计算所需样本量,以保证检验的敏感性和可靠性。
# 安装 statsmodels(如未安装)
# %pip install statsmodels
from statsmodels.stats.power import TTestIndPower
# 计算效应量(Cohen's d)
effect_size = (mean_B - mean_A) / np.sqrt((std_A ** 2 + std_B ** 2) / 2)
# 计算当前样本量下的检验功效(power)
analysis = TTestIndPower()
power = analysis.power(effect_size=effect_size,
nobs1=n_A,
ratio=n_B/n_A,
alpha=0.05,
alternative='two-sided')
print(f'当前样本量下的检验功效(power):{power:.3f}')
# 计算达到 0.8 检验功效所需的单组样本量
required_n = analysis.solve_power(effect_size=effect_size,
power=0.8, alpha=0.05,
ratio=1,
alternative='two-sided')
print(f'达到 0.8 检验功效所需的每组样本量:{int(np.ceil(required_n))}')当前样本量下的检验功效(power):1.000
达到 0.8 检验功效所需的每组样本量:12828.7.6 结果解读与业务建议
t 检验结果 如果 P 值显著低于 0.05,说明实验组和对照组的人均消费金额存在统计学意义上的差异。
非参数检验结果 P 值同样低于 0.05,则无论数据是否正态分布,结果均具有统计显著性。
业务解读
- 若实验组均值更高且显著,说明「满 40-10」方案对提升人均消费有正向效果,可考虑在更多门店推广。
- 若差异不显著,建议保留现有方案,避免无效促销带来成本浪费。
- 还应结合其它指标(如客单价、复购率、利润率)进行多维综合评价。
28.8 非随机分组实验:情境、影响与对策
A/B 测试的理想状态是将所有实验对象随机分配到各组,这样可以确保两组除了促销方案不同以外,在性别、年龄、消费习惯等一切可观测与不可观测因素上都没有系统性差异。这样才能保证我们观察到的人均消费差异,是由促销方案本身引起的,而不是由其他外部因素“混淆”了实验结论。
但在实际业务中,往往会遇到非随机分组(non-random assignment)的情形,导致样本选择偏误或自选择偏误,影响实验的内部和外部有效性。以咖啡店促销方案为例,常见的非随机分组情境包括:
28.8.1 典型情境
自选择偏误(Self-selection Bias) 例如顾客可以自行选择参与哪种促销方案。愿意选择 B 方案(满 40 减 10)的顾客可能本身消费能力较强、更愿意多消费。这使得实验组和对照组“天生不同”,即使 B 方案本身没效果,实验组人均消费也可能更高,造成促销效果被高估。
系统性分配(Algorithmic or Policy-based Assignment) 系统根据顾客历史消费金额、会员等级、性别、年龄、工作日/周末等特征进行分组。例如高活跃用户分配 B 方案、低活跃用户分配 A 方案。这使实验组的基础消费水平本来就更高,导致促销效果被高估,影响因果解释力。
参与概率不均等 某些顾客接触到促销活动的机会较多(如常驻用户或新客),分组概率并不均等。如果分析时不加控制,实验结果只代表被高频分配组的用户,而非全部用户。
28.8.2 影响分析
因果解释性丧失 分组不是完全随机时,实验组和对照组的差异不仅仅来源于促销方案,其他因素(如用户自带的高消费倾向)也会影响结果。此时对比两组人均消费金额,不能得出“方案 B 导致消费增加”的结论。
外部有效性受限 如果实验样本只覆盖特定用户群体,结论无法推广到所有门店或所有客户。
28.8.3 应对与改进策略
坚持随机分组原则 实验方案设计阶段,优先采用系统随机分配,确保每个用户分到各组的概率相等,排除人为和算法干预。
分层随机化(Stratified Randomization) 若用户本身在性别、年龄、消费能力等方面差异较大,可在这些特征层内分别进行随机分组,保证每一层次的用户在各组中比例相等。
事后加权与统计控制 若实际分组未做到完全随机,可以在分析阶段采用倾向得分加权(propensity score weighting)、回归控制等方法,尽量弥补非随机分组带来的偏误。
基线特征均衡性检验 在实验开始前后,比较实验组和对照组在性别、年龄、消费历史等关键变量上的分布情况,及时发现和修正不均衡。
28.8.4 小结
A/B 测试设计和执行阶段,分组方法决定了因果推断的科学性。一旦存在非随机分组,就可能导致样本选择偏误、自选择偏误等问题,结果解读需更加谨慎。 如发现偏误不可避免,应在报告中如实披露实验设计与样本来源的局限性,避免业务决策受到误导。
上述问题都是因果推断中的常见挑战,解决这些问题需要结合实验设计、统计方法和业务理解进行综合考虑。通过坚持随机分组原则、分层随机化、事后加权等方法,可以最大程度上提高实验结果的可靠性和解释力。
对此有兴趣的读者可以参考以下资料:
- Alves, Matheus Facure. 2022, Causal Inference for The Brave and True. Online Read, -github-
- 基本上覆盖了目前文献中使用多的多数因果推断方法,包括 IV, DID, SDID, PSM, Matching, Panel, SCM, RDD
- 提供了完整的 Python 代码,可以 Fork -github- 仓库,然后在本地运行 .ipynb 文档 (Jupyter Notebook)
- 书中使用了
causalml和dowhy两个包,前者是作者开发的一个包,后者是微软开发的一个包
- Cerulli, G. Econometric evaluation of socio-economic programs theory and applications. Springer, 2022. -Link-, -Website- (登陆学校图书馆账号可以下载 2e PDF), PDF-1e
- 共 6 章,介绍了反事实框架,回归调整法 (RA),逆概率加权 (IPW),匹配,多期 DID,合成控制法等。基本上涵盖了主流的因果推断方法。
- Chernozhukov, V. & Hansen, C. & Kallus, N. & Spindler, M. & Syrgkanis, V. (2024): Applied Causal Inference Powered by ML and AI. CausalML-book.org; arXiv:2403.02467. -PDF-,Website, github